You shall know a word by the company it keeps. (John Rupert Firth, 1957)
情報可視化の6ステップ

今日はテキストデータの可視化について見ていきます。
可視化手法については、これまでに学んだ質的データと量的データの可視化と共通する部分が多いのですが、データの用意の方法が異なります。特に、自然言語処理(Natural Language Processing)の分野で研究されている基盤技術(形態素解析や分散表現など)は、テキストデータの前処理には重要です。そのため、今回はテキストデータを用意するプロセスについて主に説明します。
コンピュータで言葉の意味を理解すること
テキストを処理する基盤技術の背景として、自然言語処理において自然言語を解析することがどのように捉えられてきたのかを紹介します。
自然言語の曖昧性
自然言語を解析するにあたっては、言語表現が二つ以上の意味や意図をもちうるという曖昧性を考えることが必要です。自然言語の曖昧性には、語彙(単語などの語を構成する要素の総体)、文、文脈(文の前後のつながり)の3つの段階が考えられます。
語彙の曖昧性
日本語や中国語、タイ語のように単語を空白で分けない(わかち書きをしない)言語は、何をもって一つの単語とみなすかという単語分割の問題があります。
Example
「法隆寺は聖徳太子によって建てられた
「によって」は一語なのか、「に+よって」のように二語に分けられるのか?
Example
「くるまでまつ」
「くるま+で+まつ」なのか、「くる+まで+まつ」なのか?
Example
「ここではきものを脱ぎなさい」
単語よりも小さな単位を語彙として考えることもあります。
Example
unknown → un(否定を表す接頭辞)+ known(形容詞)
新しさ → 新し(形容詞語幹)+ さ(接尾詞)
ここで意味を構成する最小の単位のことを形態素(morpheme)と言い、文を形態素に分割する自然言語処理の技術のことを形態素解析(morphological analysis)と言います。例えば、「食べさせました」を「食べ+させ+まし+た」と分割することで、文の構造や意味を特定しやすくします。
形態素解析はおおまかに、単語分割、品詞推定、見出し語化という3つサブタスクに分割することができます。単語分割(word segmentation)は入力の文字列を単語単位に分割する処理、品詞推定(part-of-speech tagging; POS tagging)は、単語に対して品詞を付与する処理、見出し語化(lemmatization)は、単語の正規化のために原形に変換する処理です。
Example
「28日は国立で富士通の岩倉さんから3000円借りました。」
単語分割
28/日/は/国立/で/富士通/の/岩倉/さん/から/3000円/借り/まし/た/。
品詞付与
語 品詞 28 名詞 日 名詞 は 助詞 国立 名詞 で 助詞 富士通 名詞 の 助詞 岩倉 名詞 さん 名詞 から 助詞 3000 名詞 円 名詞 借り 動詞 まし 助動詞 た 助動詞 。 記号 見出し語化
語 品詞 見出し語 28 名詞 28 日 名詞 日 は 助詞 は 国立 名詞 国立 で 助詞 で 富士通 名詞 富士通 の 助詞 の 岩倉 名詞 岩倉 さん 名詞 さん から 助詞 から 3000 名詞 3000 円 名詞 円 借り 動詞 借りる まし 助動詞 ます た 助動詞 た 。 記号 。
最初の例で見たように、何をもって一語とするかは議論があるところです。そこで、「単語」をあえて定義せず、「短単位」「長単位」といった異なる粒度の単位を設定し、ユーザが目的に合わせてそれらを組み合わせて使うという方法も考案されています。例えば、用例の収集や検索では曖昧性なく解析できる単位として「短単位」を使用し、言語的な特徴を捉えたい時は文節を基にして分割する「長単位」を用いることが考えられます。
Example
「くにたちさくらフェスティバルに参加した」
短単位
語 品詞 くにたち 名詞 さくら 名詞 フェスティバル 名詞 に 助詞 参加 名詞 し 動詞 た 助動詞 長単位
語 品詞 くにたちさくらフェスティバル 名詞 に 助詞 参加し 動詞 た 助動詞
単語分割ができたとしても、語彙の曖昧性の問題は残ります。
Example
「はしがここにある」
「はし」は「橋」なのか「箸」なのか?
「はし」「かき」「bank」などのように発音が同じで意味の異なる語は同音異義語と呼ばれ、語彙的曖昧性が生じる原因の一つです。
また、同じ語が複数の意味を持つことによって生じる曖昧性もあり、これを語彙の多義性と言います。
Example
- 太郎は明るい人だ
- 電球が明るい
- 部屋が明るい
1は性格が明るいという意味であるが、2と3は照明が明るいという意味である。
Example
- 太郎は3時に行く
- 太郎は公園に行く
- 太郎は旅行に行く
それぞれ、格助詞「に」の時に関する用法、場所に関する用法、目的に関する用法である。
「に」の用法の違いは、「明るい」の意味の違いとも違うことに注意してください。これは「明るい」と「に」の語の性質の違いによるものです。
「明るい」は内容語(content word)に分類されます。内容語とは、名詞や動詞、形容詞や副詞など具体的な内容をもつ語のことであり、時代とともに語の意味やニュアンスが変化し、新しい語が生まれやすく、語彙数が大きく変化する傾向があります。そのため、open word classとも呼ばれます。
一方で、「に」はそれ一語では意味をなさず、動詞や形容詞などの述語に対する名詞の文法的な役割を表す語であり、機能語(function word)に分類されます。機能語は、接続詞、助動詞、否定詞、代名詞、限定詞など、内容語を伴って文法的・論理的な役割や関係を表す語のことです。現代ではほぼ固定され、語彙数が増えることがないことから、closed word classとも呼ばれます。
文の曖昧性
語彙が無事に同定されたとしても、語彙動詞がどのように結びつくかについても曖昧性が生じます。これを構造的曖昧性と言います。
Example
「警官が自転車で逃げる泥棒を追いかけた」
警官が[[[自転車で逃げる]泥棒を]追いかけた]
警官が[[自転車で][逃げる泥棒を追いかけた]]
Example
I saw someone on the hill with a telescope
I [saw [someone on the hill] [with a telescope]]
I [saw [[someone on the hill] [with a telescope]]]
コンピュータで文の構造を補完し、文の構造を明らかにする処理を構文解析と言います。
Example
帽子と靴を買った → [帽子と靴]を買った
友達と靴を買った → 友達と[靴を買った]
文の曖昧性としては、スコープ(作用域)の曖昧性もあります。
Example
「私は給食を全部食べなかった」
上記の文は、否定「ない」のスコープによって意味が曖昧な文になっています。そもそも文の意味とは何かという問題についてはさまざまな考え方がありますが、有力な考え方の一つとして、文の意味とは命題(proposition)、すなわち真偽を問うことができるものである、という考え方があります。これに基づいて考えると、否定「ない」の適用範囲が「私は給食を食べる」という命題であれば、この文は「私は給食をまったく食べなかった」という意味となる一方で、適用範囲が「私は給食を全部食べる」という命題であれば、「私は給食をすべては食べず、一部残した」という意味になります。
Example
I heard that the shop was closed.
を否定する文を作ると、
[1] I heard that the shop was not closed.
[2] I did not hear that the shop was closed.
文脈の曖昧性
自然言語の曖昧性について、最後に前後の文脈や発話の状況によって意味が曖昧になるものがあります。
Example
昨日、太郎の妻と妹が家にやってきた。
この文では、「妹」が誰の妹を指すのかという点で曖昧性があり、太郎の妹を指す可能性と話者の妹を指す可能性が考えられます。もしこの文の直前に「私には妹が一人いる」などがあれば、「妹」は話者の妹を指す可能性が高まります。
Example
この教室は寒いね。
この文については、単に教室の中の気温が低いという状況を述べているのか、教室のエアコンをつけてほしいという要求を言外の意味として伝えているのか、静かな教室で話者と聞き手以外には誰もいない状況において何か話をしないと気まずいという言外の意味を伝えているのか、様々な可能性が考えられます。
分布意味論
コンピュータで自然言語を扱うには、まず言葉の意味をどのように計算可能な形式で表現するかが問題となります。自然言語処理では、主に分布意味論(distributional semantics)に基づいて言葉の意味を捉えます。
分布仮説
分布意味論では、「語の意味はそれが出現した周囲の語によって決まる」という分布仮説(distributional hypothesis)に基づいて語の意味を捉えます。分布仮説は1950年代のZelig Harrisを中心としたアメリカの構造主義言語学(structural linguistics)やJ. R. Firthを中心としたイギリスの語彙論(lexicology)を端緒とします。分布仮説に基づいて、語の意味をその語と共起しやすい(つまり、その語の周辺に現れやすい)語の出現頻度にしたがって表現する考え方が分布意味論です。
Example
- 今日の天気は晴れである。
- 今日の1時間ごとの天気、気温、降水量を掲載します。
- 今日の天気予報をお伝えします。
- 今日は天気がよいので布団を干した。
- 今日と明日の天気と風と波をみられます。
上記文集合では、「天気」という語は「今日」という語と同時に出現しやすい(「天気」と「今日」の共起頻度が高い)という傾向が見られます。分布意味論ではある語の前後に現れる語の分布のことを文脈(context)と言いますが、この文脈を使って語の意味についての特徴づけを行っています。
Example
- I drink beer.
- We drink wine.
Example
- I guzzle beer.
- We guzzle wine.
単語のベクトル化
分布意味論では、語の意味を実数値を要素とするベクトルで表現する考え方が標準的であり、ベクトル意味論(vector semantics)と呼ばれることもあります。
単語の意味をベクトルで表すための素朴な手順としては、まず自然言語の文章を集めたコーパス(何らかの目的で使用できるテキストデータ)を用意し、コーパス中の単語の前後に現れる単語列を周辺の文脈として(文脈単語)として数え上げます。コーパス中のそれぞれの単語の周辺にどんな単語が現れやすいかをカウントして得られる行列を共起行列(co-occurrence matrix)と呼びます。
例えば、「今日は晴れている」という1文のみからなるコーパスを用いて構築した共起行列は下記のようになります。
| 今日 | は | 晴れ | て | いる | |
|---|---|---|---|---|---|
| 今日 | 0 | 1 | 0 | 0 | 0 |
| は | 1 | 0 | 1 | 0 | 0 |
| 晴れ | 0 | 1 | 0 | 1 | 0 |
| て | 0 | 0 | 1 | 0 | 1 |
| いる | 0 | 0 | 0 | 1 | 0 |
共起行列の行は各単語の意味を表すベクトルをなしており、このように単語の意味をベクトルで表現したものを単語ベクトル(word vector)と呼びます。「今日」のベクトルは (0, 1, 0, 0, 0)、「晴れ」のベクトルは (0, 1, 0, 1, 0) というように、それぞれ5次元のベクトルで表現できます。
もう少し大きいコーパスから作成した共起行列の例を見てみしょう。
| 今日 | の | 天気 | … | 布団 | 気象 | |
|---|---|---|---|---|---|---|
| 今日 | 0 | 3 | 10 | … | 4 | 10 |
| の | 3 | 0 | 5 | … | 7 | 5 |
| 天気 | 10 | 5 | 0 | … | 6 | 1 |
| … | … | … | … | … | … | … |
| 布団 | 4 | 7 | 6 | … | 0 | 6 |
| 気象 | 10 | 5 | 1 | … | 6 | 0 |
この共起行列を見ると、「天気」と「気象」は似たようなベクトルになっています。意味の近い単語は似たような単語ベクトルに対応していることが分かります。
2つの単語の意味がどれくらい近いか遠いかという類似度(similarity)の計算は、情報検索や質問応答といったさまざまな自然言語処理のタスクで使われていまし、私たちの思考の中でも使われます。例えば、Londonに対してParisとFrance間と同じ関係が成り立つ語はUnited Kingdomであるというように、私たちはある単語や単語間の関係から、類似するほかの単語や単語間の関係を考えることができます。
分布意味論では、2つの単語ベクトルを比較することで、単語間の類似度を計算することができます。単純な方法としては、2つの単語ベクトル の内積 をとる方法があります。2つの単語ベクトルが同じ向きで大きな値をとるほどこの値は大きくなり、単語の意味が類似していると言えます。しかし、頻出する単語はより大きな値の単語ベクトルを持ち、そのため内積も大きくなるため、頻度とは関係なく単語間の類似度を計算するために内積をベクトルの大きさで割ることで正規化するコサイン類似度(cosine similarity)が広く使用されています。
テキストデータの用意
テキストデータの前処理
テキストデータの前処理には主に以下のステップが含まれます。これは、おおまかに自然言語の語彙の曖昧性の解消と文の曖昧性の解消に対応しています。
- 形態素解析
- 単語分割
- 品詞付与
- 原形抽出
- 構文解析
文脈の曖昧性を解消するためには、語の意味を理解することが必要であるため、これはベクトル化後に初めて行えるタスクだと言えます。
テキストデータのベクトル化
文書のベクトル表現:Bag of Words
文書をベクトル化する方法として、Bag of Words(BoW)があります。文書中に出現するユニークな語にインデックスを割り当て、各単語が文書中に何度出現したかを数え上げます。出現頻度を対応する単語のインデックスに割り当てることで文書ベクトルを作成します。
最も単純なBoWでは出現頻度を使いますが、tf-idfという単語の重要度を考慮した指標を用いることもあります。シンプルですが、文書の特徴を捉えることができます。
語のベクトル表現:分散表現
前節の「単語のベクトル化」で紹介した手法です。処理の方法をコードで見ていきましょう。
テキストデータの可視化
ここでは、Bag of Wordsの可視化手法を3つ紹介します。
ワードクラウド

共起ネットワーク
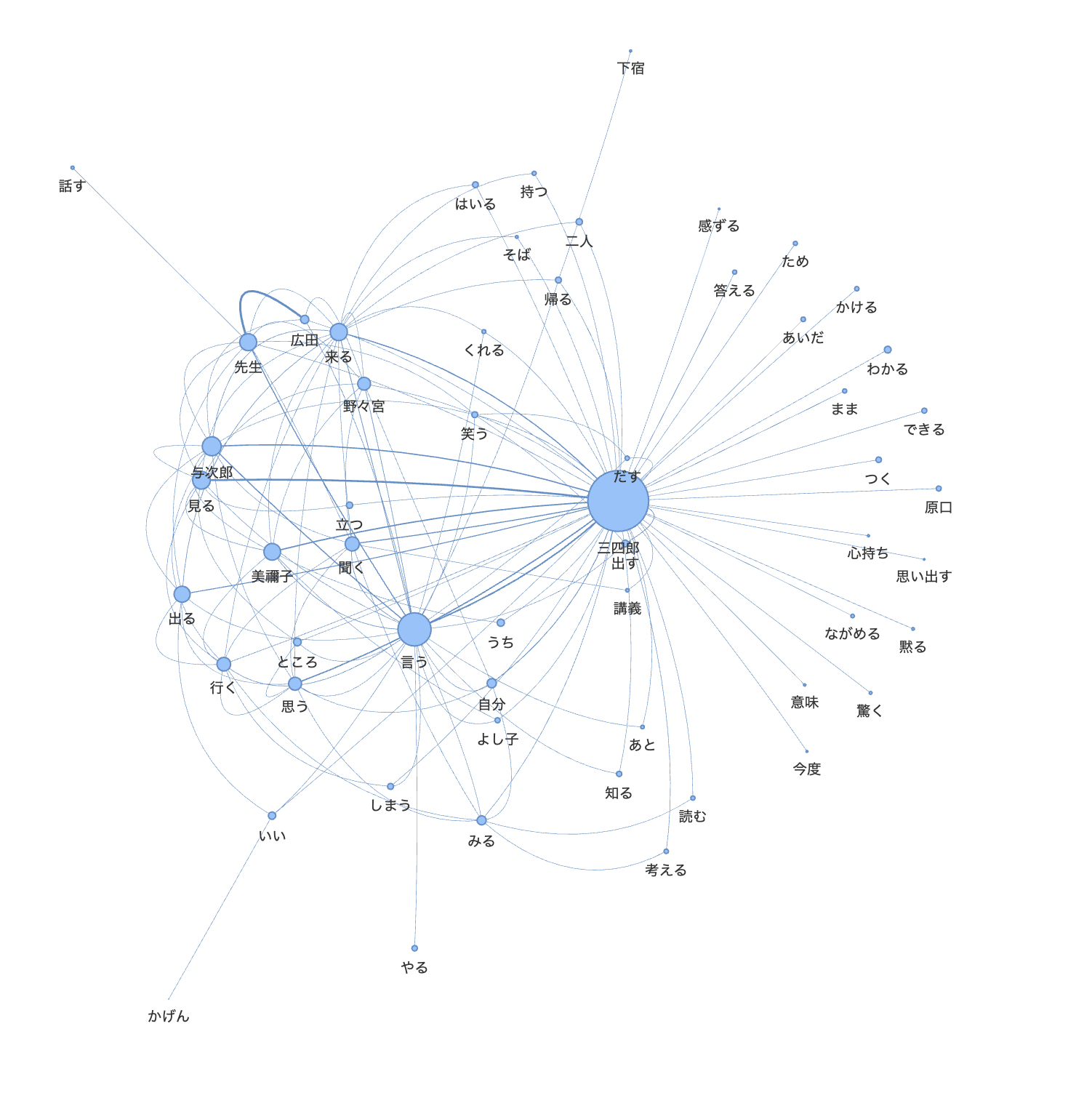
共起ヒートマップ